[7] Network Flow
The Maximum-Flow Problem
生活中常用圖形Graph來描述網路交通問題(transportation networks),其edges可用來攜帶交通量(carry flow),而nodes則扮演路由點(switches)連接不同edges。Network模型當中有幾項組成元素:edges上的capacities,表示可攜帶量;node source產生交通量,node sink吸收交通量;最後是traffic本身,會在edges當中被傳遞。
Flow Networks
flow network是一有向圖G = (V,E),且有以下特點:
- 每條邊都e都有其capacity,為一正數,用Ce表示。
- 圖中的點有單一起始點source(s)。
- 圖中的點有單一終點sink(t)。
- 除了source、sink之外的點稱為internal nodes。
假設:
- 沒有邊流入source;沒有邊流出sink。
- 每個node至少都有一edge相鄰。
- 所有capacity皆為整數。
Defining Flow
定義何謂carry traffic or flow。
s-t flow 是一function f,映射每一條edge到一個非負實數,f : E->R+;f(e)代表edge e可攜帶的flow容量。並且flow f 滿足下列兩項特性:
- Capacity Conditions(容量限制):在所有E當中的邊e, 皆符合 0 ≤ f(e) ≤ Ce.
- Conservation conditions(守恆) :對於除了s、t外的所有點v,所有流進v的邊e Σf(e) = 所有流出v的邊e Σf(e)
The Problem
給定一flow network,一個自然的目標就是安排traffic來最有效率地使用可得資源:
Given : a flow network
Output:a flow of maximum possible value
觀察這一問題,可以用問題本身的架構去找到s-t flow的上限值。假設將G分為兩集合A和B,使得s∈A;t∈B。那麼可直覺理解當一flow要從s到t,勢必得在某一時刻從A到B,因此會被一條edge的capacity所設定上限。這表示圖形中的每一條 cut 會設定flow可能的上限值。
Design Algorithm
初始時,設定f(e) = 0 for all e。
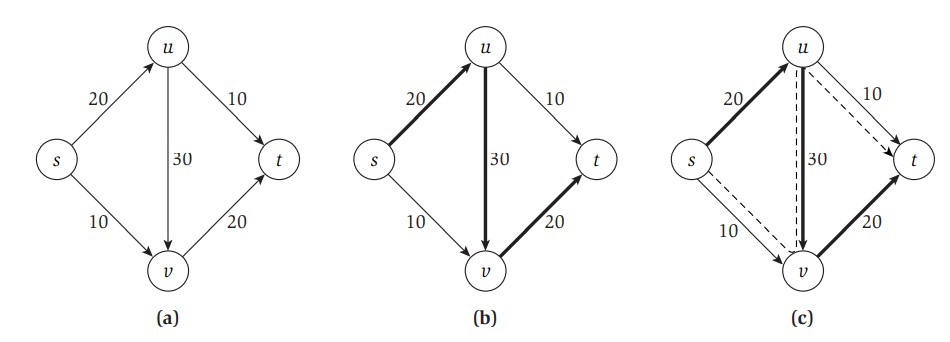
首先嘗試"push" flow從s到t,path由{(s,u) , (u,v) , (v,t)}組成。挑選最大可通過量20,並更新這些edge的f(e)=20,沒用到的其他兩條就維持0。現在我們的flow值維持在20,這樣是最大可能的值嗎?不!因為可能值是30。問題出在 — 我們目前執著於想要僅用一條s-t路徑直接push完所有flow(在不超過各邊限制下)。
因此做些改變,我們看(c)當中的虛線部分,push 10從s到v,造成v不守恆(流入20+10;流出20),因此我們 取消操作(undo)10從u到v,如此確保v的守恆,但是變成u不守恆(流入20;流出10),因此我們push 10從u到t。
將上述操作整理一下,可知
- 我們可以push forward 剩餘可通過流量(leftover),最直覺的作法。
- 我們可以push backward已經有攜帶流量的邊,來分散不同方向的流量。
The Residual Graph
藉由上面可以push forward & backward的特性,我們定義一圖Gf(Residual Graph),並有以下特性:
Gf和G的node 集合會是一樣的。
forward edges:e = (u,v) in Gf, 其容量為Ce - f(e)(leftover)。
因為在e = (u,v) in G中,已有f(e)被使用,因此在Gf會是Ce - f(e)。
backward edges : e' = (v,u) in Gf,其容量為f(e)。
因為在e = (u,v) in G中,已有f(e)被使用,因此可以 undo的量為f(e)。
根據上面定義,我們可以知道在Gf當中的邊數量可能會是G的兩倍,且通常我們會稱residual graph中的capacity為residual capacity,以跟原始G當中的容量capacity做區別。
Augmenting Paths
現在我們要確切地定義一條Gf當中可由s-t的flow。
- 令P為Gf當中一條simple path s-t,也就是說P不會到同一點超過一次。
- 定義bottleneck(P,f)為P當中最小的minimum residual capacity(respect to f)。
- 接者我們定義一操作稱為augment(f,P),其會在G當中產生新的flow f ' 。
augment(f,P)
Let b = bottleneck(P,f)
For each edge (u,v)∈P
If e=(u,v) is a forward edge then
increase f(e) in G by b
Else ((u,v) is a backward edge, and let e=(v,u))
decrease f(e) in G by b
Endif
Endfor
Return f
Ford-Fulkerson Algorithm
Max-Flow
Initially f(e)=0 for all e in G
While there is an s-t path in the residual graph Gf
Let P be a simple s-t path in Gf
f′ = augment(f,P)
Update f to be f′
Update the residual graph Gf to be Gf′
EndWhile
Return f
Maximum Flows and Minimum Cuts
將G分為兩集合A和B,使得s∈A;t∈B。那麼可直覺理解當一flow要從s到t,勢必得在某一時刻從A到B。正式說法
- s-t cut是點集合V的(A,B)分割(partition),使得s∈A;t∈B。
- cut (A,B)的容量以c(A,B)表示,指的是加總所有從A流出的邊的flow值:c(A,B) = Σ(e out of A) Ce(為最粗淺的上界)。
定理1
令f為任意s-t flow;(A,B)為任意s-t cut。那麼v(f) = f out(A) - f in(A)。v for value。
這個定義比一般的簡單上界更強。可藉由觀察流經cut的flow量測flow值。計算方式為 總離開A的量 - 總迴旋回(swirls back into)A的量。
證明
根據定義v(f) = f out(s)。假設 f in (s) = 0,當s沒有流入的邊時,我們可以寫成v(f) = f out(s) - f in(s)。因為A當中除了s之外的點v都是中介點,可知f out(v) - f in(v) = 0。最終可以寫成
ν(f) = v∈A Σ(f out(v) − f in(v))。因為裡面唯一不為0的值就是當node被設為s時。
試著把等式右邊做修改。考慮一edge e於下面四種情況
e的兩端都在A:f(e)會是加總一次+和一次-的結果,相互抵消。
e的尾端在A:+。
e的頭部在A:-。
e的兩端都不在A:根本就不在加總裡。
v∈A Σ(f out(v) − f in(v)) = e out of AΣf(e) - e into AΣf(e) = f out(A) - f in(A)
定理2
延續自定理1。
因為A、B是相對的關係(流出A的 = 流進B的),因此定裡1可以變成下面:
令f為任意s-t flow;(A,B)為任意s-t cut。那麼v(f) = f in(B) - f out(B)
定理3
延續自定理1、2。
若A = V-{t}且B={t},那麼定理2=v(f) = f in(B) - f out(B) = f in(t) - f out(t)。已假設t沒有流出的值:f out(t)=0,因此我們可以定義flow值等於f in(t),也就是最後流入sink t的總量。
定理4
令f為任意s-t flow;(A,B)為任意s-t cut。那麼ν(f) ≤ c(A, B)。
證明
ν(f) = f out(A) − fin(A) [定理1]
≤ f out(A) [f in(A)≥0]
= e out of A Σ f(e)
≤ e out of A Σ Ce [容量限制]
= c(A, B)
定理4看似比定理1薄弱,然而定理4的右手邊為C(A,B)和特定的flow f無關。其意義為 每一個flow的上限值都被每一個cut的容量所界定。也就是說:
- 給定一G中一s-t cut值C',我們可以馬上知道G中不存在一s-t flow可以大於C'。
- 給定一G中一s-t flow值v',我們可以馬上知道G中不存在一s-t cut可以大於v'。
Analyze Algorithm:Max-Flow = Min-Cut
令f'表示一Ford-Fulkerson回傳的flow。希望證明f'是G當中flow的最大可能值。用上一節所討論的方式,欲證明有一s-t cut(A',B')使得v(f') = c(A' , B')。此演算法終止條件是flow f在residual graph Gf中沒有s-t path,這也是唯一需要的特性來證明該f是最大可能值。
定理1
若 f 是一s-t flow使得沒有s-t path存在於Gf,那麼G當中便存在一s-t cut(A',B')使得v(f) = c(A',B')。於是f是G當中最大可能的flow值,且(A',B')有G當中任意s-t cut的最小容量。
證明
上面敘述聲稱 「存在一cut滿足一我們想要的特性」。現在要證明cut確實存在。
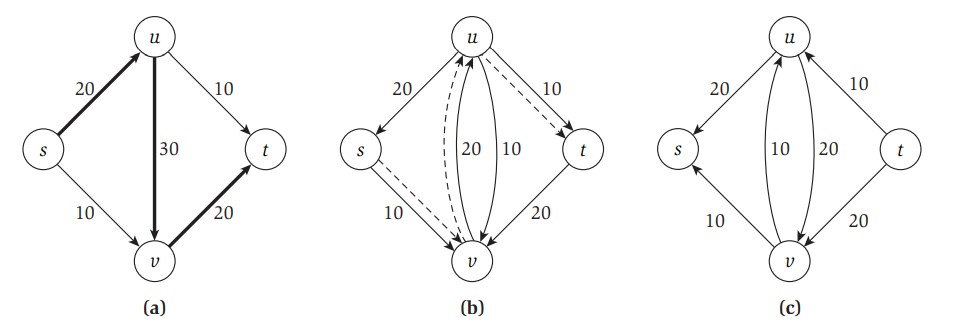
令A' 表示滿足在Gf中有s-v path的所有點v;令B'表示剩下的點,B' = V - A'。參照下圖:
- (A',B')確實是一s-t cut。s ∈ A',因為總是有路徑可從s-s。此外,t ∉ A,因為在residual graph中沒有s-t路徑,因此,t ∈ B'。
- 假設e = (u,v)是G中的一邊,其中u ∈ A'且v ∈ B'。我們聲稱f(e) = Ce。若否,e會是Gf當中的forward edge,且因為u ∈ A',Gf存在一s-u path,再加上e會在Gf形成s-v path,違反一開始v ∈ B'的假設。
- 假設G中存在e' = (u',v'),其中u' ∈ B;v' ∈ A。我們聲稱f(e') = 0。若否,e'會在Gf中造成backward edge e'' = (v',u'),且因為v' ∈ A',在Gf中存在s-v' path,再加上e''會在Gf形成s-u' path,違反一開始u' ∈ B'的假設。
根據上面的釐清,可知,f'吸收了所有flow值(所有流出A'的邊);所有流入A'的邊都是沒用的,結論:
v(f) = f out(A') - f in(A')
= e out of A' Σ f(e) - e into A' Σf(e)
= e out of A’ Σ c(e) - 0
= c(A' , B')